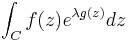Method of steepest descent

For the optimization algorithm, see Gradient descent.

In mathematics, the method of steepest descent or stationary phase method or saddle-point method is an extension of Laplace's method for approximating an integral, where one deforms a contour integral in the complex plane to pass near a stationary point (saddle point), in roughly the direction of steepest descent or stationary phase. The saddle-point approximation is used with integrals in the complex plane, whereas Laplace’s method is used with real integrals.

The integral to be estimated is often of the form

\displaystyle \int_Cf(z)e^{\lambda g(z)}dz

where C is a contour and λ is large. One version of the method of steepest descent deforms the contour of integration so that it passes through a zero of the derivative g′(z) in such a way that on the contour g is (approximately) real and has a maximum at the zero.

The method of steepest descent was first published by Debye (1909), who used it to estimate Bessel functions and pointed out that it occurred in the unpublished note Riemann (1863) about hypergeometric functions. The contour of steepest descent has a minimax property, see Fedoryuk (2001). Siegel (1932) described some other unpublished notes of Riemann, where he used this method to derive the Riemann-Siegel formula.

Extensions and generalizations

An extension of the steepest descent method is the so-called nonlinear stationary phase/steepest descent method. Here, instead of integrals, one needs to evaluate asymptotically solutions of Riemann–Hilbert factorization problems.

Given a contour C in the complex sphere, a function ƒ defined on that contour and a special point, say infinity, one seeks a function M holomorphic away from the contour C, with prescribed jump across C, and with a given normalization at infinity. If ƒ and hence M are matrices rather than scalars this is a problem that in general does not admit an explicit solution.

An asymptotic evaluation is then possible along the lines of the linear stationary phase/steepest descent method. The idea is to reduce asymptotically the solution of the given Riemann–Hilbert problem to that of a simpler, explicitly solvable, Riemann–Hilbert problem. Cauchy's theorem is used to justify deformations of the jump contour.

The nonlinear stationary phase was introduced by Deift and Zhou in 1993, based on earlier work of the Russian mathematician Alexander Its. A (properly speaking) nonlinear steepest descent method was introduced by Kamvissis, K. McLaughlin and P. Miller in 2003, based on previous work of Lax, Levermore, Deift, Venakides and Zhou. As in the linear case, steepest descent contours solve a min-max problem.

The nonlinear stationary phase/steepest descent method has applications to the theory of soliton equations and integrable models, random matrices and combinatorics.

References